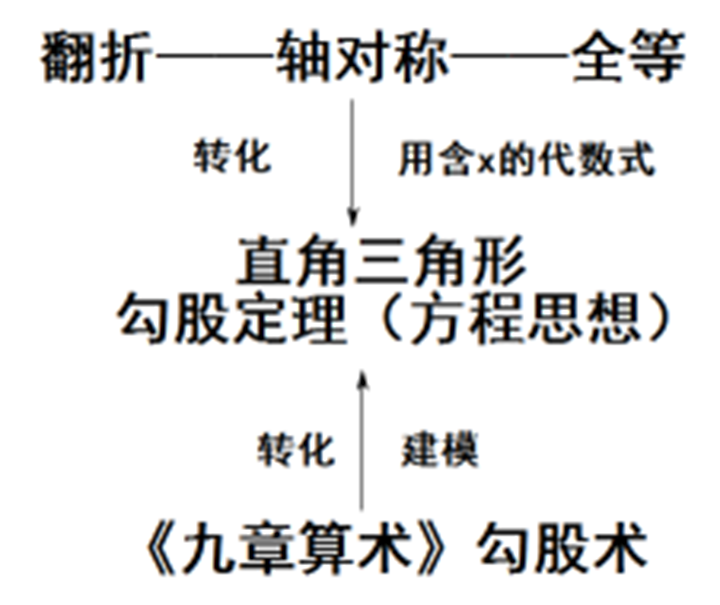
一、教学目标

1.将实际问题转化为数学问题，建立数学模型，体会与勾股定理有关的方程思想、分类讨论等数学思想方法.

2.完善基于勾股定理问题解决的认知结构，提高理性思考的层次，积累解决与勾 股定理相关问题的解题自信.

3.感受与勾股定理相关的数学文化，提高学习数学的兴趣.

二、教学重点与难点

1.重点：用方程的视角看勾股定理.

2.难点：与勾股定理有关的分类讨论与建模.

三、教学过程

第一环 始于生活中的数学——从一张纸开始

• 一张纸，你知道它的长和宽之比吗？你有怎样的方法可以验证呢？

百科链接：

（2）小组展示：

一张8cm长为和宽为6cm的长方形纸片，（或自己设定长方形纸片的长和宽），以点C为例，你还可以有哪些折叠的方法(一次折叠)，使点C落在比较特殊的位置.画出翻折后的图形，可以求出哪些线段的长. （每个小组至少发现一种翻折后的图形）

第二环  领略古代数学家的勾股情结

评价机制：完成1题（合格）；完成2题或学会两题（良好）；

能够进行展示讲解，初步形成解决问题的认知结构（优秀）；

      以上都可以完成并自主完成能力提升（特优）

题目1：今有一竖立着的木柱，在木柱的上端系有绳索，绳索从木柱上端顺木柱下垂后，堆在地面的部分尚有尺.牵着绳索退行，在离木柱根部尺时，地面绳索用尽，问绳索长是多少？选自《九章算术》卷九勾股篇 第七题

题目2：今有墙高丈.倚木杖木杖于墙，使木之上端与墙平齐，牵引木杆下端退一尺，则木杆（从墙上）滑落至地上.问木杆长是多少？选自《九章算术》卷九勾股篇第八题

第三环 小组小结

四、作业设计

1、能力提升

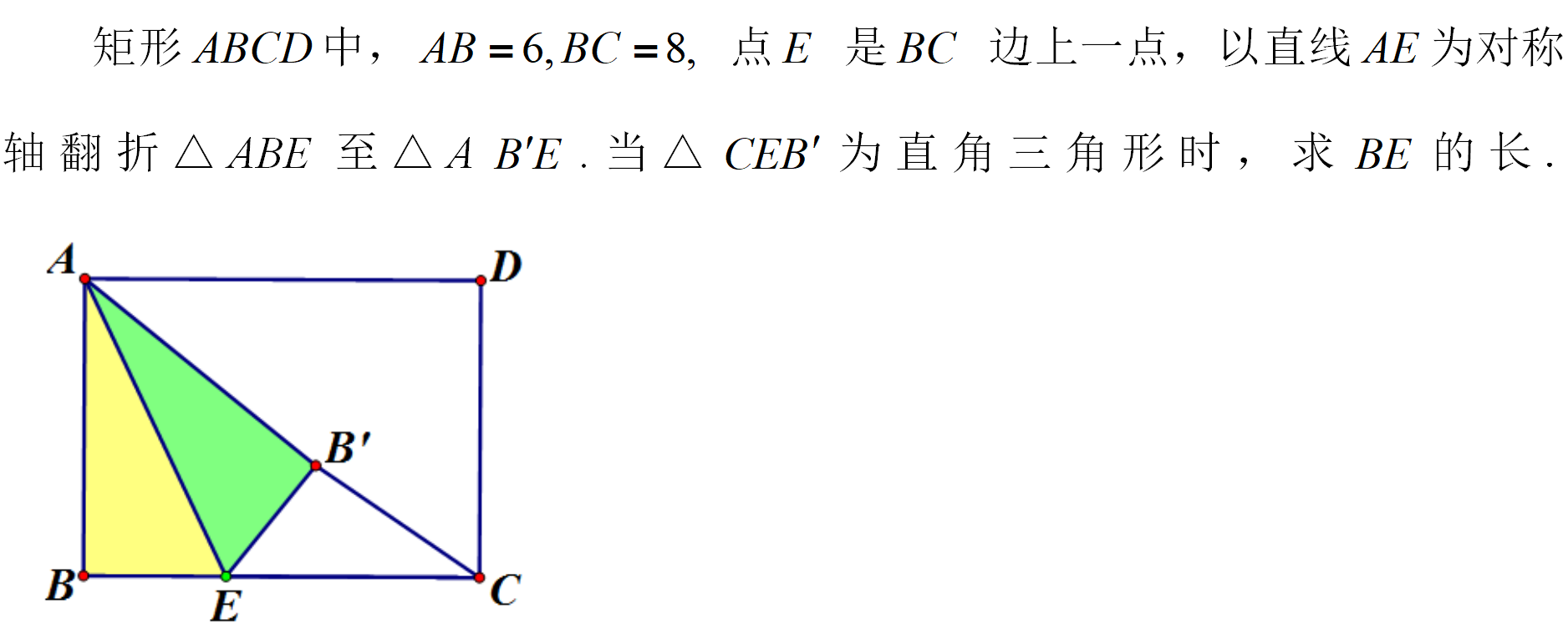
2、数学好玩

3、（2015•浙江省台州市，第8题）如果将长为6cm，宽为5cm的长方形纸片折叠一次，那么这条折痕的长不可能是（  ）

1. 8cm      B. 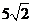cm   C. 5.5cm       D. 1cm

4、（2014•山东潍坊，第18题）我国古代有这样一道数学问题：“枯木一根直立地上，高二丈周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”

题意是：如图所示，把枯木看做一个圆柱体，因一丈是十尺，则该圆柱高为尺，地面周长为尺，有葛藤子点处缠绕而上，绕五周后其末端恰到达处，则问题中葛藤的最短长度是_______尺.

五、板书设计