18.1 函数的概念
上海市位育初级中学 费晓芳
[教学目标]
1、知道数量、变量与常量的意义,并能在具体问题中认识并分清变量和常量;
2、在具体情境中,用运动变化的观点看待事物,理解变化过程中的两个变量之间的相互依存,初步理解函数概念,初步感受变化与对应的思想;
3、在参与变量的发现和函数概念的形成过程,提高观察、概括、分析问题和解决问题的能力;
4、探索实际问题中的数量关系,感受现实生活中函数的普遍性,初步感受函数的应用价值。
教学重点:结合具体实例归纳、概括函数的概念
教学难点:初步理解函数的概念
[教学过程]
一、课题导入——两分钟预备铃观看视频
在刚才的视频中,我们感受到了四季的变化、日出和日落、怒放的花朵、舞蹈中律动的节奏,可见,我们生活在一个充满运动的世界里,万事万物都在不断运动变化着。为了更好地认识世界,改造世界,我们不妨从数学的角度来研究身边的运动。
设计意图:通过观看记录日常生活中的变化过程的视频,让学生感受到自己其实生活在一个充满运动变化的世界,要学会用运动变化的观点去观察事物。而函数正是体现运动变化的基本数学概念,它从数值角度刻画事物变化的过程,表达变量之间的变化联系。
二、创设情境,观察概括
情境1 视频《加油的过程》(观看过程中随意按暂停键)
问题1 在汽车加油的过程中,涉及了哪些量?
此处用体积描述油量,用金额描述汽油的单价和总价。在认识和描述某一事物时,经常会用像时间、面积、速度、温度、长度、体积等来具体表达事物的某些特征(属性),称之为“量”,同时我们用“数”来表示量的大小。数与度量单位合在一起,就是我们常说的“数量”。
问题2 在加油这个变化的过程中,哪几个量发生了改变?哪几个量没有发生改变?
油量和总价一直在不停地变化着,可以取不同的数值,像这样的量叫做变量。而单价一直保持数值不变,是6.51,像这样的量叫做常量。在汽车加油的过程中,汽油的单价是一个常量,始终是6.51,而油量和总价是两个变量,他们不断变化着。为了方便描述,不妨用字母表示变量,用x表示油量即变量x,用y表示总价即变量y。
问题3 在变化的过程中,两个变量总价y和油量x有怎样的联系或规律?
这两个变量之间相互联系,相互影响。当加油量越多时,所花费的总价就越高,也就说变量y是随着变量x的变化而变化。
问题4 在这个变化的过程中,随着变量x取一个值,总价y的值可以确定吗?(在演示过程中,随意按暂停键,取几对数值,用列表呈现)
可见,运动是绝对的,静止是相对的。这样的y值有几个?
当变量x取一个确定的值时,变量y的值也随之唯一地确定。概括而言,这两个变量之间的关系是变而变,定而唯一定。像这样的两个变量之间的关系,描述为变量y与变量x之间存在确定的依赖关系。
设计意图:通过加油站加油时的总价和加油量的直观数据看,可以强烈感受到变化的量、不变的量,以及两个变量之间的相互依存相互变化的关系,并在最后通过几个数据的暂停,感受到随着自变量的确定,因变量也随之唯一确定。
情境2 本班级三位男生100米赛跑的运动过程(随意按暂停键)
问题1 在这个赛跑的过程中,涉及了哪些量,哪些是变量,哪些是常量?
路程是常量,从情境得知,100米跑,路程因此确定,时间和平均速度是变量
问题2 在100米赛跑过程中,时间t和平均速度有着怎样的联系或规律?
在百米跑中,时间随着平均速度的变化而变化,跑得越快则用时越少;跑得越慢,则用间越多。
问题3 如果知道某个学生100米跑的平均速度,他的百米赛跑时间唯一确定,吗?
现在知道生1、生2、生3的平均速度,通过填表,容易看出当变量v取一个确定的值时,变量t的值也随之唯一确定,这两个变量之间也存在确定的依赖关系。
设计意图:通过播放三位学生的录像视频,进一步感受变量之间的相互依存/相互依赖,感受运动变化思想和对应的思想。
情境3 陈艾森在里约奥运会上勇夺10米跳台冠军跳水运动的视频
这是我国跳水健儿陈艾森在里约奥运会上勇夺10米跳台冠军时的场景,下面,从数学的视角来观察这个跳水运动的变化过程。通过慢动作回放,可以发现,在陈艾森完成这个跳水动作的过程中,起跳后的时间在变化,他离水面的高度在变化(手比划),他离开跳台的水平距离也在变化,就有三个变量,这里只研究起跳后的时间变量和离水面的高度变量这两个变量。现在以入水点为坐标原点,起跳后的时间为横轴,他离水面的高度为纵轴,建立一个平面直角坐标系。如果把他的身体抽象成一个点的话,那他完成这套跳水动作的过程的运动轨迹是怎样的?学生所描述的跳水轨迹就是这个图形。
师:如果我们取到图上一个点,这个点的纵坐标表示的是什么?
生:是他的离水高度
师:那这时它的横坐标对应的是什么?
生:起跳后的时间
师:在这个变化过程中,h有没有随着t的变化而变化?
生:有
师:它们之间存在着确定的依赖关系吗?
生:不太确定
师:当我们取定一个t时,能找到唯一确定的h,这时候变量间有没有确定的依赖关系?
生:有
设计意图:学生能够理解生活中离水面的高度随着时间的变化而变化,当时间确定了,离水面的高度也被唯一。课堂上,对于用图像表示的函数关系中,纵坐标的值随着横坐标的值的变化而变化,学生理解起来有困难。于是借助跳水运动,先从生活的视频中感受,再用几何画板把它抽象成抛物线,让学生进一步感受到横坐标和纵坐标之间也存在依赖关系。
三、概括归纳,引出课题
像上述三个情境中,凡此变数中函彼变数者,则此为彼之函数。这节课,研究什么是函数?(引出课题:18.1(1)函数的概念)
问题1 三个情境中的变量有什么范围限制吗?
在汽车加油的过程中,x取20L呢?100L能取满吗?由生活经验得知,加油量x必须满足0≤x≤油箱体积;
百米赛跑中, 0<变量v≤世界纪录。可见,变量是在一个被允许的范围内变化的,所以,两个变量是在变量x的允许取值范围内,变量y随着x的变化而变化,当变量x取一个确定的值时,y的值随之唯一确定,如果满足上述条件,我们就称:变量y叫做变量x的函数,其中x是自变量,y是因变量,函数的自变量允许取值的范围叫做这个函数的定义域。
问题2 三个情境中,哪两个变量是函数关系?谁是自变量和因变量?
问题2变式 加油时,人们有时会说:加200元或300元的油,此时哪两个变量是函数关系?谁是自变量和因变量?为什么?
设计意图:同样是加油,可以按照油量加油,也可以按照金额加油,谁是自变量、谁是因变量由考虑问题的视角而定,不是一成不变的。
问题3 为什么研究函数呢?
师:通过前面的情境,可以发现函数是用来研究两个变量之间的变化规律的一种工具。通过研究两个变量之间的函数关系,人们可以知道因为速度不够,所以跑得慢,就可以针对性地去做一些速度练习。再如,我们知道要取得跳水的高分,其中一项就是要使入水时的水花尽可能小,这就意味着在一定高度时跳水运动员就要完成跳水动作,让自己的身体完全打开,并垂直于水面入水。有了函数这个工具,只要研究离水面高度和起跳时间的变化关系,教练员就可以指导运动员在什么时候完成动作、什么时候打开身体,最终帮助运动员问鼎奖杯。
设计意图:让学生理解为什么要研究函数,目的是研究规律,为生活服务,感受到数学的魅力。
问题4 从数学的角度如何描述函数关系?
(1)在之前的三个变化过程中,通过列表容易发现两个变量之间确定的依赖关系,这种表示方法称为列表法。
(2)用数学式子,如y=6.51x,,这种表达两个变量之间依赖关系的数学式子称为函数解析式。
(3)在跳水的过程中,图像也可以描述两个变量之间的函数关系,称为图像法,之后会进一步做具体研究。
四、概念辨析
辨析1:当x取下列值时,求x+2的值

设计意图:求代数式的值也蕴含函数关系,只是需要用运动变化的观点来看问题。这道题设计的目的是在以往的知识中更好地理解函数。 师:这就是七年级学习的求代数式的值的问题,对于代数式x+2,给定x的一个值,可以求出这个代数式的一个值。如果x是一个变量,那么,x+2也是一个变量。请问:变量x+2是不是变量x的函数?
辨析2:下图是某日的气温变化图,一天中什么时候气温最低?什么时候最高?气温随着时间的变化而变化,温度T是时间t的函数吗?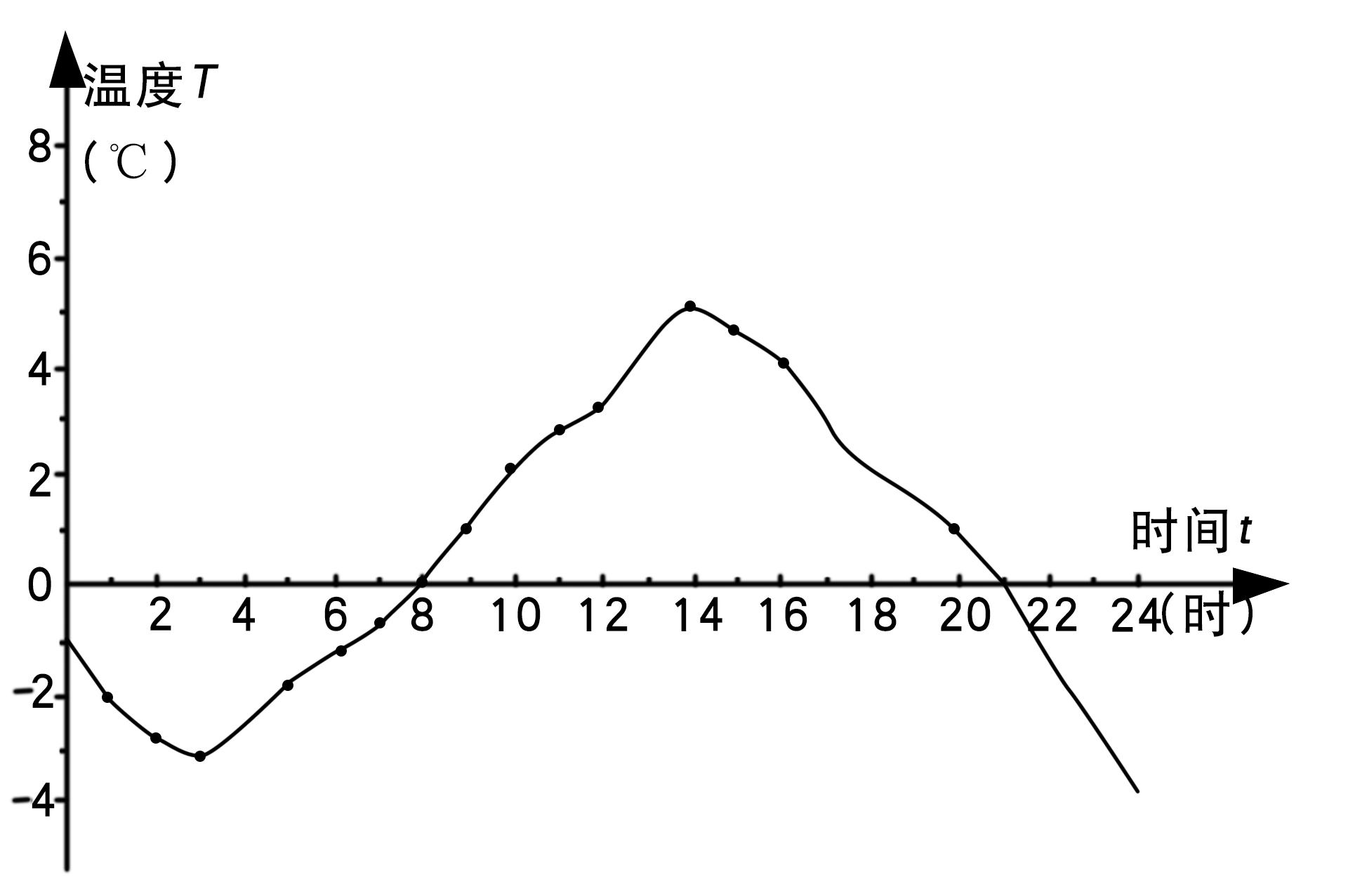
设计意图:借助跳水运动从生活实际的理解,到用几何画板把它抽象成函数的图像表示(抛物线),学生已经感受到,在图像法表示中,横坐标和纵坐标之间也存在依赖关系,此题就不难理解了。
辨析3:在跳水运动中,时间t秒是不是他的离水高度h米的函数?
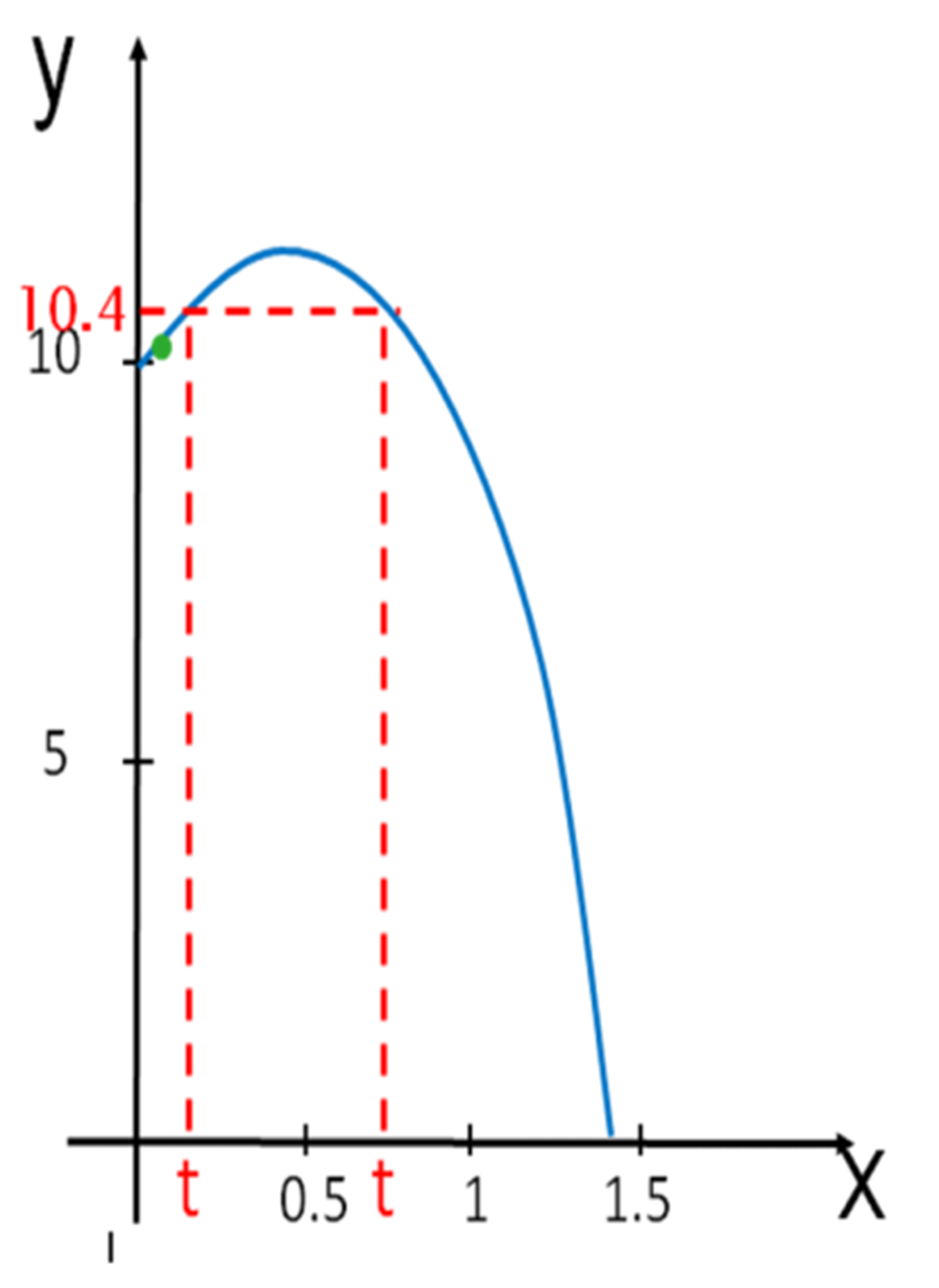
设计意图:为了让学生理解随着自变量的确定,因变量只有 唯一确定的值和它对应,所以给出一个反例。如图,当离水高度为10.4米时,有两个时间点与之相对应,所以时间t秒不是离水高度h米的函数,为高中的对应说打下基础。
五、归纳小结
1、什么是函数?
2、为什么要学函数?
六、课后作业
巩固练习:阅函数的发展史。
实践练习:找找日常生活中遇到的其它具有函数关系的例子,并交流。





