20.1 一次函数的概念 教学设计

上海市位育初级中学 乔越

教学目标：

• 类比正、反比例函数的方法进一步研究一次函数，理解一次函数的概念；
• 掌握用待定系数法确定一次函数的解析式，了解一次函数与正比例函数、常值函数 的关系，从中感悟“从特殊到一般”的思想方法；
• 经历从具体问题到数学概念的抽象过程，感受数学建模思想，初步体会k和b的实际意义.

教学重点：

理解一次函数的概念；

教学难点：

体会k和b的实际意义

教学过程设计：

1.概念引入

活动 1：回顾所学函数

师：同学们，在之前的学习中，我们已经学习了函数，那我们就一起先来回顾一下

    请同学说说看，什么是函数?

生：两个变量之间的依赖关系，研究变量之间随变而变的变化规律

师：我们曾经学过哪些具体的函数？

生：正比例函数和反比例函数

师：那么在学习这两类具体函数的时候，我们又学习了它的哪些内容?

生：解析式，定义域，图像

师：没错，首先，我们都是通过解析式的特征来给具体的函数下定义的；

当这里的比例系数k未知时，我们通常会通过待定系数法来求解析式

由于正比例函数和反比例函数都只有一个系数k，所以在代入时只需要一组对应值。

除此之外，我们还往往会利用图像的直观来研究函数的性质。

今天这节课，我们又将要学习一类具体的函数，在这之前，我们先从生活中找找他的影子

概念初建：

活动 2: 创设问题情境，在变化过程中研究规律，建立函数关系

①情境1：小明每天早上坐车去学校.在行驶的过程中，小明了解到车每行驶1km耗油0.2 L

师：请问在这个情境中，你找到了哪些变量

生：行驶路程，所用油量，剩余油量

如果油箱原有120 L汽油，观察动画

师：我们还能找到什么变量？

生：剩余油量，

师：随着行驶路程增加，剩余油量怎么变化？

生：随着路程增加，剩余油量减少

填表格 对应显示图片

（追问0.2——按照这个程度变化的，追问120——初始值）

师：设剩余油量，请问与路程x之间的变化规律如何表示？

生:  y2=120-0.2x（板书）

②情境2：物理课上,侍老师拿了一个弹簧，弹簧挂上物体后会伸长，测到弹簧的长度y（cm）与所挂物体质量x（kg）有下面的关系：

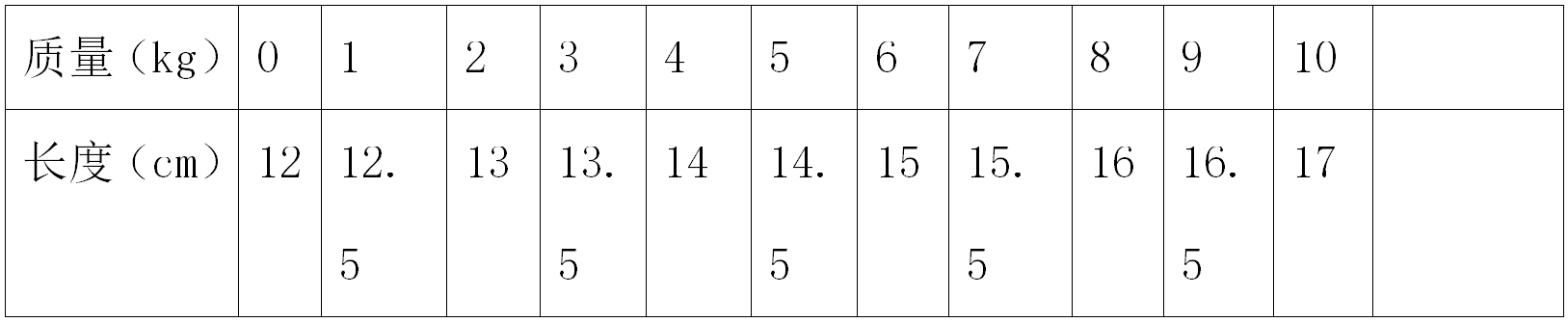
师：随物体质量的增加，长度如何变化?

生：随着质量增加，长度也增加

师：按照什么程度增加

生：当质量每增加1kg时，长度增加0.5cm

师：你是从哪里（哪些值）看出来的？

师：那么在这个过程中，若设质量为xkg，长度为ykg

学生得到弹簧总长y（cm）与所挂物体质量（kg）的函数关系式。

   （板书）

追问：这里12是？

③数学课上，给定一根长为16厘米的细绳，请将它刚好围成一个长方形，若长方形两条邻边分别设为cm和cm，请问关于的函数关系式：

y=8-x（板书）

设计意图：创设三个实际情境，从生活实际到代数、几何图形，以探索变化规律为背景，让学生经历从生活中找出常量与变量建立四个函数模型的过程，发展学生的建模数学思想，体会数学知识来源于实际生活，激发学生学习数学、解决实际问题的兴趣。

概念形成：

活动3:学生观察这四个函数等号右侧的这些代数式，有没有共同特征？

——整式→一次整式

从特殊到一般，请同学们根据这样的特征，用一个的解析式来概括出来

设计意图：通过观察共同特征，归纳出一次函数的本质特征，感受数学的简洁之美，体会抽象思想以及学习新知的必要性。

生：可以用来表示．（追问k）

师：给这种函数取个名字，可以叫做什么函数？

生：一次函数

师：非常好，今天这节课我们就来聊聊一次函数，请同学们说说什么是一次函数？

生成概念：

活动4：利用课前复习的表格，类比正比例函数和反比例函数的学习，得到一次函数的定义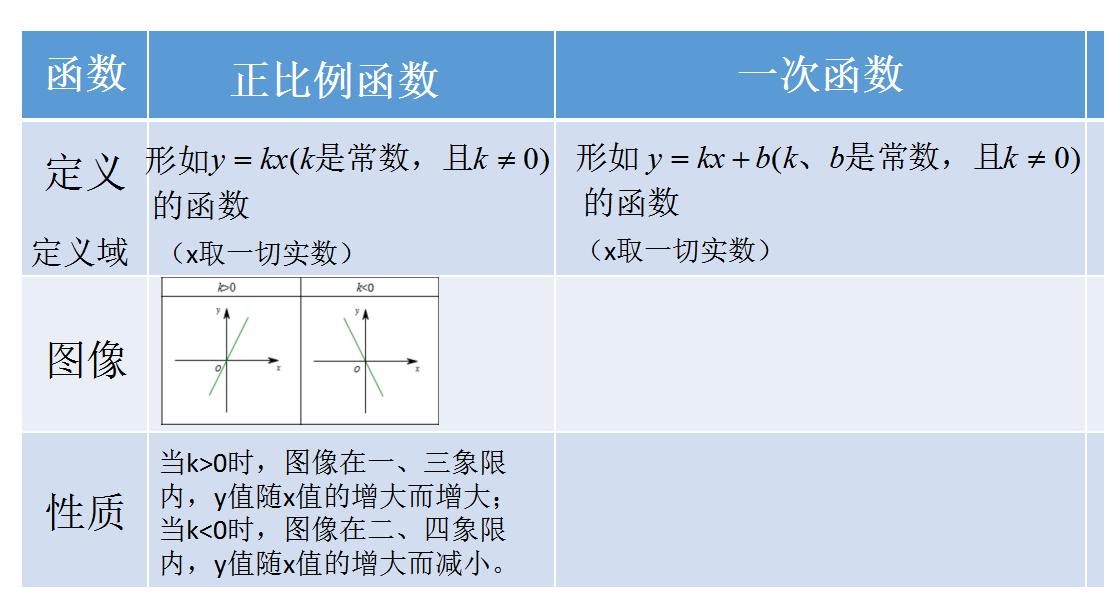

请学生比较一次函数和正比例函数的解析式，说说区别与联系，感悟正比例函数是一次函数的特例。

同时板书，明确一次函数与正比例函数之间一般特殊的关系以及常值函数概念：

设计意图：类比正比例函数的概念，对解析式中的参数与进行讨论，明确其代数意义，特殊情况下常值函数概念，以及从一般到特殊的正比例函数。同时类比学习正比例函数和反比例函数，一次函数的定义域是一切实数。

概念深化：

师：好，明确了概念，看看同学们能否火眼金睛，判断接下来的函数解析式是不是我们今天学习的一次函数

活动5：概念辨析：

根据变量x，y 的关系，判断 y 是否是 x 的一次函数．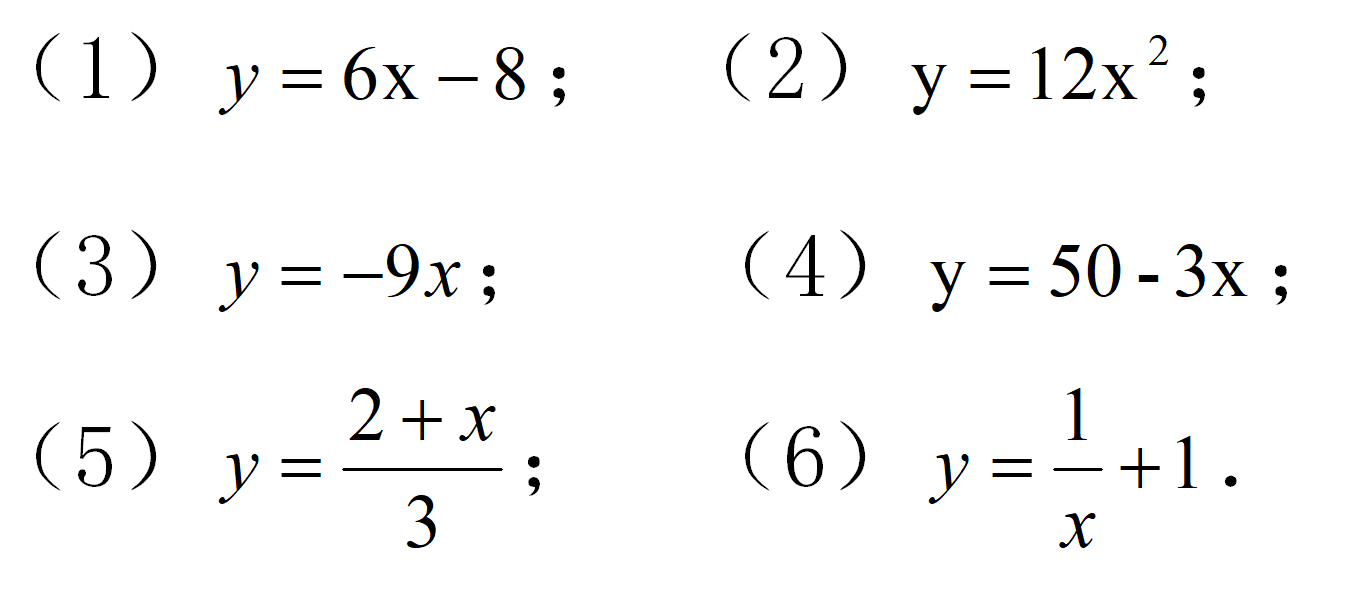

师：通过刚刚的练习，相信同学们现在已经掌握了一次函数的解析式，那接着让我们来一起聊聊一次函数的定义域，

回顾情境1、2、3刚刚从解析式的角度分析，我们知道一次函数的定义域是一切实数

师：，但当它涉及具体情境时，为了让函数反映出变量在有效的范围内的变化规律，我们要根据实际意义来确定自变量的取值范围。

活动6：已知一次函数： （m为常数）

(1)当m____________时，y与x是正比例函数关系 .

(2)当x=3，y=0时，求m的值.

（注意板书，尤其强化舍与不舍问题）

设计思路：强化≠0以及一次函数与正比例函数的联系与区别

师：所以观察一个解析式是不是一次函数，我们不光要从形式上观察，还有特别留意k≠0的大前提，以及b=0从而得到正比例函数的这种特殊情况

师：学以致用，接下来我们一起回到生活中的情境

活动8：

一次函数的应用

温度通常有两种度量单位：摄氏度（记为℃）和华氏度（记为℉）。已知摄氏度和华氏度之间是一次函数关系，如图温度计中提供了部分数据的对应关系

师：你从题目中读到了什么？

生：摄氏度和华氏度是一次函数的关系

师：联想到什么？

生：设一次函数的一般形式y=kx+b(k≠0)

读图 师：读图中四组数据，随着x的变化，y按照什么程度变化？

请学生在操作单上求解析式

展示学生操作单 选取任意两组数据的——用待定系数法求解析式

选取0，32的 选取的好处？b的意义

学会感受变化程度，根据k、b实际意义得到解析式的

课堂小结：

师：请问同学们这节课我们学到了什么？

生：1一次函数的概念——解析式与定义域

追问：解析式中要注意：k≠0

      你了解k、b的实际意义吗？变化程度 初始值

      定义域在实际情境中要根据实际意义考虑

      正比例函数和一次函数的区别联系

• 请同学们想想这节课我们学到哪些方法，比如通常情况下我们会用待定系数法求具体的解析式，当然有时候我们也可以直接从情境中感受到变化程度，从k、b的实际意义得到解析式
• 再想想：为我们又是如何为一次函数下定义的——模仿（类比）了正比例函数得到了一次函数的概念

师：可以根据解析式的形式来给具体的函数下定义，在以后的学习过程中，比如当右边的代数式是二次整式时，我们还会继续用这个方法来学习二次函数。

也有同学提到了正比例函数与一次函数的关系，当初始值为0时，它是一个正比例函数，当初始值不为0了，它就是一个一次函数，正比例函数是一次函数的特例，这里就蕴含着一种数学思想：从简单到复杂，从特殊到一般，很多时候，我们就是在用这样的方式在认识世界，寻找普遍规律。

师：今天我们认识了一次函数的概念，请同学们猜猜看，明天我们会从什么角度学习一次函数？

生：图像、性质

师：太聪明了，接下爱我们还将从数形结合的观点来研究一次函数，感受k和b的意义。

希望同学们学习一类函数，也学会学习函数的方法，尝试多用数学来解决实际问题。